贪心算法
基本概念
所谓贪心算法是指,在对问题求解时,总是做出在当前看来是最好的选择。也就是说,不从整体最优上加以考虑,它所做出的仅仅是在某种意义上的局部最优解。
贪心算法没有固定的算法框架,算法设计的关键是贪心策略的选择。必须注意的是,贪心算法不是对所有问题都能得到整体最优解,选择的贪心策略必须具备无后效性(即某个状态以后的过程不会影响以前的状态,只与当前状态有关。)
所以,对所采用的贪心策略一定要仔细分析其是否满足无后效性。
基本思路
- 建立数学模型来描述问题
- 把求解的问题分成若干个子问题
- 对每个子问题求解,得到子问题的局部最优解
- 把子问题的解局部最优解合成原来问题的一个解
存在问题
- 不能保证求得的最后解是最佳的
- 不能用来求最大值或最小值的问题
- 只能求满足某些约束条件的可行解的范围
贪心算法适用的问题
适用前提:局部最优策略能导致产生全局最优解。
实际上,贪心算法适用的情况很少。一般对一个问题分析是否适用于贪心算法,可以先选择该问题下的几个实际数据进行分析,就可以做出判断。
贪心算法的实现框架
从问题的某一初始解出发: while (朝给定总目标前进一步) { 利用可行的决策,求出可行解的一个解元素。 } 由所有解元素组合成问题的一个可行解;
背包问题
问题:【背包问题】有一个背包,容量是 M=150,有 7 个物品,物品可以分割成任意大小。要求尽可能让装入背包中的物品总价值最大,但不能超过总容量。 物品: A B C D E F G 重量:35 30 60 50 40 10 25 价值:10 40 30 50 35 40 30
| 物品 | A | B | C | D | E | F | G |
|---|---|---|---|---|---|---|---|
| 重量: | 35 | 30 | 60 | 50 | 40 | 10 | 25 |
| 价值: | 10 | 40 | 30 | 50 | 35 | 40 | 30 |
分析: 目标函数: ∑pi 最大 约束条件是装入的物品总质量不超过背包容量:∑wi<=M( M=150) (1)根据贪心的策略,每次挑选价值最大的物品装入背包,得到的结果是否最优? (2)每次挑选所占重量最小的物品装入是否能得到最优解? (3)每次选取单位重量价值最大的物品,成为解本题的策略 值得注意的是,贪心算法并不是完全不可以使用,贪心策略一旦经过证明成立后,它就是一种高效的算法。比如,求最小生成树的 Prim 算法和 Kruskal 算法都是漂亮的贪心算法。 贪心算法还是很常见的算法之一,这是由于它简单易行,构造贪心策略不是很困难。 可惜的是,它需要证明后才能真正运用到题目的算法中。 一般来说,贪心算法的证明围绕着:整个问题的最优解一定由在贪心策略中存在的子问题的最优解得来的。 对于例题中的 3 种贪心策略,都是无法成立(无法被证明)的,解释如下: 贪心策略:选取价值最大者。反例:
W=30
物品:A B C
重量:28 12 12
价值:30 20 20
根据策略,首先选取物品 A,接下来就无法再选取了,可是,选取 B、C 则更好。
(2)贪心策略:选取重量最小。它的反例与第一种策略的反例差不多。
(3)贪心策略:选取单位重量价值最大的物品。反例:
W=30
物品:A B C
重量:28 20 10
价值:28 20 10
根据策略,三种物品单位重量价值一样,程序无法依据现有策略作出判断,如果选择 A,则答案错误。但是果在条件中加一句当遇见单位价值相同的时候,优先装重量小的,这样的问题就可以解决.
所以需要说明的是,贪心算法可以与随机化算法一起使用,具体的例子就不再多举了。(因为这一类算法普及性不高,而且技术含量是非常高的,需要通过一些反例确定随机的对象是什么,随机程度如何,但也是不能保证完全正确,只能是极大的几率正确)。
集合覆盖问题
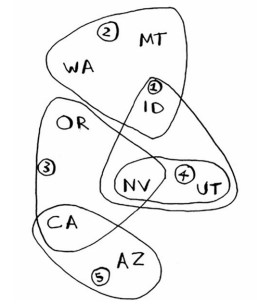
集合覆盖问题: 选择最少的集合,覆盖全部的元素。 假设你办了个广播节目,要让全美 505050 个州的听众都收听得到。为此,你需要决定在哪些广播台播出。在每个广播台播出都需要支付费用,因此你力图在尽可能少的广播台播出。现有广播台名单如下。
| 广播台 | 覆盖的州 |
|---|---|
| (1) KONE | ID,NV,UT |
| (2) KTWO | WA,ID,MT |
| (3) KTHREE | OR,NV,CA |
| (4) KFOUR | NV,UT |
| (5) KFIVE | CA,ZA |
如何找出覆盖全美 505050 个州的最小广播台集合呢? 最容易考虑到的可能是暴力求解法:列出每一种可能的广播集合(可能的子集有 2n2^n2 n 个);在这些集合中选出能覆盖全美 505050 个州的最小集合数。假设每秒可筛选出 101010 个子集,其花费的时间如下:
没有任何算法可以足够快地解决这个问题!怎么办呢?使用贪婪算法可以得到非常接近的解。
- 选出这样一个广播台,即它覆盖了最多的未被选择的州。即便这个广播台覆盖了一些已经选择的州,也没有关系;
- 重复第一步,直到覆盖了所有的州。
贪婪算法是不错的选择,它们不仅简单,而且通常运行速度很快。在这个例子中,贪婪算法的运行时间为 O(n2)O(n^2)O(n^2),其中 n 为广播台数量。
解决上述问题的代码如下:
- 第一步:准备工作:构建数据结构;
- 用集合 states_needed 存储所有的州;
- 用字典表示电视台 stations 的覆盖面;
states_needed = set(['mt', 'wa', 'or', 'id', 'nv', 'ut', 'ca', 'az']) # 包含要覆盖的州
stations = {} # 存储电视台集合
stations["kone"] = set(["id", "nv", "ut"])
stations["ktwo"] = set(["wa", "id", "mt"])
stations["kthree"] = set(["or", "nv", "ca"])
stations["kfour"] = set(["nv", "ut"])
stations["kfive"] = set(["ca", "az"])
final_stations = set() # 存储最终电视台的集合
2
3
4
5
6
7
8
9
10
- 第二步:利用贪心算法求解最少的电视台
- 选出这样一个广播台,即它覆盖了最多的未被选择的州。我们将这个广播台存储在 best_station 中;
- 重复第一步,直到覆盖了所有的州。
while states_needed:
best_station = None # 最佳电视台:覆盖了最多未覆盖的州
states_covered = set() # 最佳电视台与未覆盖州集合的交集
for station, states in stations.items():
covered = states_needed & states # 当前广播台与未覆盖州集合的交集
if len(covered) > len(states_covered):
states_covered = covered
best_station = station
states_needed -= states_covered # 更新未覆盖州的集合
final_stations.add(best_station) # 添加贪心算法选择的电台
2
3
4
5
6
7
8
9
10
11
最终打印的结果可能如下:
print(final_stations)
# set(['ktwo', 'kthree', 'kone', 'kfive'])
2
暴力求解算法 和 贪心算法 求解时间对比:

NP 完全问题
对于 NP 完全问题的定义,百度百科是这样给出的:NP 完全问题(NP-C 问题),是世界七大数学难题之一。 NP 的英文全称是 Non-deterministic Polynomial 的问题,即多项式复杂程度的非确定性问题。简单的写法是 NP=P?,问题就在这个问号上,到底是 NP 等于 P,还是 NP 不等于 P。
通俗地来说,有些计算问题是确定性的,比如加减乘除之类,你只要按照公式推导,按部就班一步步来,就可以得到结果。但是,有些问题是无法按部就班直接地计算出来的。一般这种无法按部就班计算出来的问题,只能通过穷举法等暴力的方法来解决。
如何识别 NP 完全问题
既然 NP 完全问题是多项式复杂程度的非确定性问题,简言之就是难解决的问题,自然也是难判别的。
其实,根本没有一个定理来判断一个问题是否是 NP 完全问题。只是,还是有很多线索可以帮助我们来做识别的。这些线索罗列如下:
- 元素较少时算法的运行速度非常快,但随着元素数目的增加,速度会变得非常慢。
- 涉及“所有组合”的问题通常是 NP 完全问题。
- 不能采用分治法的思想将大问题分解成小问题,必须考虑各种可能情况,这很可能是 NP 完全问题。
- 如果问题涉及“序列”或“集合”,并难以解决,很可能就是 NP 完全问题。
- 如果问题可转换为旅行商问题或集合覆盖问题,那就肯定是 NP 完全问题。
用最少数量的箭引爆气球
https://leetcode-cn.com/problems/minimum-number-of-arrows-to-burst-balloons/ 在二维空间中有许多球形的气球。对于每个气球,提供的输入是水平方向上,气球直径的开始和结束坐标。由于它是水平的,所以纵坐标并不重要,因此只要知道开始和结束的横坐标就足够了。开始坐标总是小于结束坐标。
一支弓箭可以沿着 x 轴从不同点完全垂直地射出。在坐标 x 处射出一支箭,若有一个气球的直径的开始和结束坐标为 xstart,xend, 且满足 xstart ≤ x ≤ xend,则该气球会被引爆。可以射出的弓箭的数量没有限制。 弓箭一旦被射出之后,可以无限地前进。我们想找到使得所有气球全部被引爆,所需的弓箭的最小数量。
给你一个数组 points ,其中 points [i] = [xstart,xend] ,返回引爆所有气球所必须射出的最小弓箭数。
示例 1:
输入:points = [[10,16],[2,8],[1,6],[7,12]] 输出:2 解释:对于该样例,x = 6 可以射爆 [2,8],[1,6] 两个气球,以及 x = 11 射爆另外两个气球 示例 2:
输入:points = [[1,2],[3,4],[5,6],[7,8]] 输出:4 示例 3:
输入:points = [[1,2],[2,3],[3,4],[4,5]] 输出:2 示例 4:
输入:points = [[1,2]] 输出:1 示例 5:
输入:points = [[2,3],[2,3]] 输出:1
